Страховая статистика

Страховая статистика показатели

Основные показатели страховой статистики

 

 

Широкое использование страховой статистики в практике актуарных расчетов вызывает необходимость в определении этого
понятия.
Страховая статистика показатели представляет собой систематизированное изучение и обобщение наиболее массовых и типичных страховых операций на основе обработки обобщенных итоговых натуральных и стоимостных показателей, характеризующих страховое дело. Все показатели страховой статистики, подлежащие статистическому изучению, делятся на две группы: отражающие процесс формирования и отражающие процесс использования страхового фонда. В наиболее обобщенном виде показатели страховой статистики можно свести к анализу следующих показателей:
е — число страховых случаев;
п — число объектов страхования;
m — число пострадавших объектов;
ЕР— сумма собранных страховых платежей;
XQ — сумма выплаченного страхового возмещения;
XSn — страховая сумма для любых объектов страхования;
?Sm — страховая сумма, приходящаяся на поврежденные
объекты.
На основе аналитических рассматриваются расчетные данные показателей страховой статистики. Частота страховых событий е/n показывает, сколько страховых случаев приходится на один объект страхования. Опустошительность страхового события (коэффициент кумуляции риска) т/е показывает, сколько пострадавших объектов приходится на страховой
случай.
Коэффициент (степень) убыточности (ущербности): XQ/ISm < 1. Превышение единицы означало бы уничтожение всех застрахованных объектов более чем один раз. Средняя страховая сумма на один объект (договор) страхования ESn/n рассчитывается как отношение страховой суммы всех объектов страхования к числу объектов страхования.
Объекты имущественного страхования обладают различными страховыми суммами. Поэтому в актуарных расчетах применяются различные методы подсчета средних величин. Средняя страховая сумма на один пострадавший объект равна страховой сумме пострадавших объектов, разделенной на число этих объектов, то есть SSn/m.
Каждый из пострадавших объектов страховой совокупности имеет свою индивидуальную страховую сумму, которая отклоняется от средних величин. Расчет этих средних величин имеет большое практическое значение в показателях страховой статистики.
Отношение средних страховых сумм называется в практике страхования тяжестью риска, которое выражается как (ESm/m) : (ESn/n). С помощью этого отношения производится оценка и переоценка частоты проявления страхового события в показателях страховой статистики.
Убыточность страховой суммы (вероятность ущерба) равна сумме выплаченного страхового возмещения, разделенной на страховую сумму всех объектов страхования, то есть EQ/ESn.
Показателем величины риска является число меньше единицы. Обратное соотношение недопустимо, так как это означало бы недострахование. Убыточность страховой суммы можно также рассматривать как меру величины рисковой премии в показателях страховой статистики.
Норма убыточности — это соотношение суммы выплаченного страхового возмещения к сумме собранных страховых платежей:
(EQ/IP) • 100 %.
Для практических целей исчисляют нетто-норму убыточности и брутто-норму убыточности в показателях страховой статистики. Полученный показатель может быть меньше, больше или равен единице. Величина нормы убыточности свидетельствует о финансовой стабильности данного вида страхования.
Частота ущерба исчисляется как произведение частоты Страховых случаев и опустошительности:
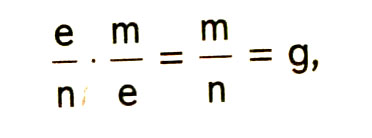где g — частота наступления страхового случая.
Частота ущерба всегда меньше единицы. При показателе частоты, равном единице, налицо достоверность наступления данного события для всех объектов. Частота ущерба обычно выражается в процентах.
Страховая статистика показатели требует, чтобы были установлены факторы, оказавшие влияние на частоту ущерба. Влияние отдельных факторов является предпосылкой образования рисковых групп.
Тяжесть ущерба. Если в результате несчастного случая застрахованному имуществу причинен ущерб, равный его действительной стоимости, то такой ущерб принято называть полным. Однако в большинстве случаев ущерб может быть меньше действительной стоимости имущества, которое не уничтожено, а только повреждено. Такой ущерб принято называть частичным в показателях страховой статистики.
Понятие тяжести ущерба можно выразить математически как отношение средних страховых сумм:
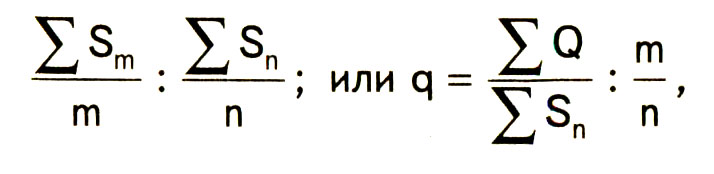где q — тяжесть ущерба, делимое — вероятность ущерба (убыточность страховой суммы), делитель — частота ущерба.


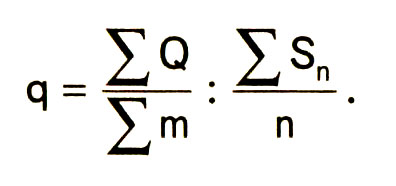Тяжесть ущерба, связанная с наступлением страхового случая, в любом виде страхования обусловлена особенностями объекта страхования. Поскольку частота ущерба показывает объекты страховой совокупности, которые повреждены в результате проявления риска, то тяжесть ущерба показывает среднюю арифметическую величину убытка (среднего обеспечения) по поврежденным объектам страхования к отношению к средней страховой сумме всех объектов:
Тяжесть ущерба, которую иногда называют степенью, объемом или размером ущерба в показателях страховой статистики, вероятностью распространения ущерба, показывает, какая часть страховой суммы уничтожена.
С помощью страховой статистики изучаются частота ущерба и убыточность по каждой рисковой группе. Статистическими методами учитываются причины ущерба и их распределение во времени и пространстве. При анализе страховая статистика должна быть обработана с учетом инфляции страховых возмещений. Обычю, чтобы получить более правдоподобную картину потенциалыых будущих убытков, прошлые убытки необходимо существеню увеличить в показателях страховой статистики.
Однако чем существеннее это увеличение для старых страховых случаев, тем более недостоверными становятся исправленные статистические данные. Серьезные сомнения по поводу использования старых Страховых возмещений имеются не только по причине шфляции, но и потому, что общая рисковая ситуация, как например, в страховании ответственности владельцев автотранспорта радикально изменилась в показателях страховой статистики.
Как следствие, страхователи при анализе предпочитают брать толькэ недавние страховые случаи, что ведет к новым трудностям: новейшие статистические данные не только менее содержательны из-за меньшего количества страховых возмещений, но, что еще хуже я серьезней, часто проходит много лет, прежде чем страховые случаи улаживаются и становится известной окончательная стоимость Страховых возмещений. Это так называемое явление запаздывающего возмещения вынуждает также корректировать исходные статистические данные в показателях страховой статистики.
Таким образом, перед актуарием стоит дилемма: если он учтет данные слишком многих прошлых лет, надежность статистики пострадает из-за включения в нее и последующего увеличения старых, нерепрезентативных убытков; если же он возьмет данные слишком свежие, надежность опять пострадает из-за уменьшения количества страховых случаев и сомнительных коррекций страховых юзмещений по незавершенным страховым случаям.
Еще одной причиной того, что старые статистические данные могут не подходить для будущего, является изменение тарифа и (или» состава портфеля.
В показателях страховой статистике обычно различают данные, характеризующие объем страховой деятельности (суммарные страховые ответственности, премии, количество рисков, суммарные застрахованные зарплаты), и данные, описывающие статистические сущности (количество страховых случаев, суммарные величины страховых возмещений, результаты (прибыли).
Из данных двух категорий часто формируются относительные показатели страховой статистики:

Количество страховых случаев
------------------------------------—--------------= Частота страховых случаев;
Объем

Суммарная величина страховых возмещений
-------------------------------------------------------------------------- =Убыточность;
Объем

Резуультат
--------------- = Рентабельность
Объём


Исправления в показателях страховой статистики, необходимые при изменении тарифа или состава портфеля, влияют в основном на объем. Следовательно, для увеличения (или сокращения) старых объемов вводится некоторый индекс (вес). Следующая причина ухудшения статистики — крупные страховые возмещения (появляются они или, наоборот, отсутствуют). Поэтому иногда приходится исключать из показателей страховой статистики чрезвычайно большое страховое возмещение или вводить его искусственно. Размер и состав страхового портфеля могут создавать еще одну статистическую проблему, поскольку нельзя считать классы рисков одновременно большими и однородными. Подводя итог, можно сказать, что для получения репрезентативной модели на будущее исходные статистические данные приходится корректировать в соответствии: ¦ с инфляцией; ¦ изменениями уровня премий; ¦ запаздыванием сообщений о страховых случаях; ¦ изменениями структуры портфеля; ¦ большими и чрезвычайными страховыми случаями. Данные факторы необходимо учитывать и при финансовом анализе страховщика и показателей страховой статистики.